티스토리 뷰
F-검정은 두 집단의 분산(흩어진 정도)이 같은지 다른지를 검증하는 통계 기법이다.
보통 t-검정·회귀분석 등 “등분산 가정”이 필요한 분석을 하기 전, 또는 공정의 품질 관리·실험 설계에서 조건별 변동성을 비교할 때 가장 많이 쓰인다.
1. F-검정이란 무엇인가?
F-검정(F-test)은 두 집단의 표본 분산을 비교해서, 모분산이 같다고 볼 수 있는지 통계적으로 검정하는 방법이다.
- 귀무가설 H₀: 두 집단의 모분산은 같다 (σ₁² = σ₂²)
- 대립가설 H₁: 두 집단의 모분산은 다르다 (σ₁² ≠ σ₂²) 또는 한쪽이 더 크다
검정통계량은 아래처럼 계산한다.
F = s₁² / s₂²
- s₁² : 분자가 되는 집단의 표본분산
- s₂² : 분모가 되는 집단의 표본분산
일반적으로 값이 더 큰 분산을 분자에 두어 F값이 1 이상이 되게 만든 뒤, F분포표(또는 소프트웨어 결과)의 임계값과 비교한다.
2. F-검정이 필요한 이유 – “분산부터 먼저 체크”
실무에서 많은 통계 기법이 두 집단의 분산이 같다(equal variance) 는 가정을 깔고 출발한다.
대표적인 예:
- 독립 2표본 t-검정(등분산 가정)
- **일원분산분석(One-way ANOVA)**에서 집단 간 분산 동질성 가정
- 단순한 회귀분석에서 오차의 분산이 일정하다는 가정(등분산성)
이 가정이 틀리면,
- p-value가 왜곡되고
- 신뢰구간이 부정확해지며
- “차이가 있다/없다”에 대한 의사결정이 잘못 될 수 있다.
그래서 **t-검정이나 ANOVA를 돌리기 전에 “분산부터 F-검정으로 살펴본다”**는 흐름이 자주 사용된다.
3. 주요 사용 예시 4가지
3-1. 생산 공정 A라인 vs B라인 품질 안정성 비교
- A라인: 샘플 30개 측정, 분산 s₁²
- B라인: 샘플 30개 측정, 분산 s₂²
두 라인의 불량 편차/품질 편차가 비슷한지 보려면 평균 차이뿐 아니라 변동성도 중요하다.
- H₀: 두 라인의 품질 변동성은 같다
- H₁: 두 라인의 품질 변동성이 다르다
F-검정 결과 p<0.05라면,
“B라인의 공정이 A라인보다 변동이 크니, 설비 튜닝·작업자 교육·원자재 편차 등에 대한 추가 원인 분석이 필요하다” 라는 식의 해석과 액션으로 연결된다.
3-2. 신약/신제품 테스트 – 조건별 반응의 안정성 확인
예를 들어 신약 임상에서
- 그룹1: 기존 치료
- 그룹2: 신약
효과의 평균 차이를 비교하기 전에, 반응 분산이 같은지를 F-검정으로 본다.
- 분산이 비슷하면 → 등분산 가정 t-검정 사용
- 분산이 다르면 → Welch t-검정(이분산 t-검정) 사용
이렇게 “검정 방식 선택”의 기준으로 F-검정을 쓴다.
3-3. 실험 설계(DOE)에서 최적 조건 선정
실험 설계에서는 평균값뿐 아니라 변동이 작은 조건을 선호하는 경우가 많다.
예) 열처리 온도 2조건(800°C, 850°C)에서 강도 측정
- 평균 강도는 비슷하지만,
- 800°C에서 분산이 훨씬 작다면 → 공정 안정성 측면에서 800°C가 더 유리할 수 있다.
이때 F-검정으로
- “두 온도 조건의 분산 차이가 통계적으로 의미 있는 수준인지”
- “실제로 공정 조건을 바꿀 만큼 변동 차이가 큰지”
를 판단해 의사결정에 활용한다.
3-4. 서비스 업종에서 점포 간 고객대기시간 변동 비교
콜센터/매장/병원 등에서 고객 대기시간 데이터를 수집하면 평균 대기시간뿐 아니라 일별 편차가 중요하다.
- 점포1과 점포2의 평균 대기시간은 거의 같아도,
- 한 점포의 분산이 훨씬 크다면 고객 체감 품질은 더 나쁘다.
이때도 F-검정으로
“어느 점포가 더 안정적인 운영을 하고 있는지” 정량적으로 비교할 수 있다.
4. F-검정의 전제 조건과 주의점
4-1. 정규성 가정
F-검정은 각 집단의 데이터가 정규분포를 따른다는 가정 하에서 이론적으로 타당하다.
샘플 수가 많고 분포가 크게 치우치지 않으면 실무에서도 어느 정도 유연하게 쓰지만, 데이터가 극단적으로 비대칭이면 다음을 고려할 수 있다.
- 로그 변환, 제곱근 변환 등으로 분포를 가까이 맞춘 뒤 F-검정
- 또는 Levene 검정, Brown–Forsythe 검정 같은 정규성에 덜 민감한 동질성 검정을 사용
4-2. 이상값(Outlier)에 민감
분산 자체가 이상값에 매우 민감하기 때문에, F-검정 역시 극단값이 하나 들어가면 결과가 왜곡될 수 있다.
그래서 실전에서는,
- 먼저 박스플롯/산점도로 이상값 확인
- 데이터 입력 오류·측정 오류 등을 제거
- 진짜 공정의 특성이라면 별도 분석 후 F-검정 해석
의 순서로 접근하는 게 좋다.
5. 엑셀/통계툴에서 F-검정 사용하는 법(간단 요약)
5-1. 엑셀
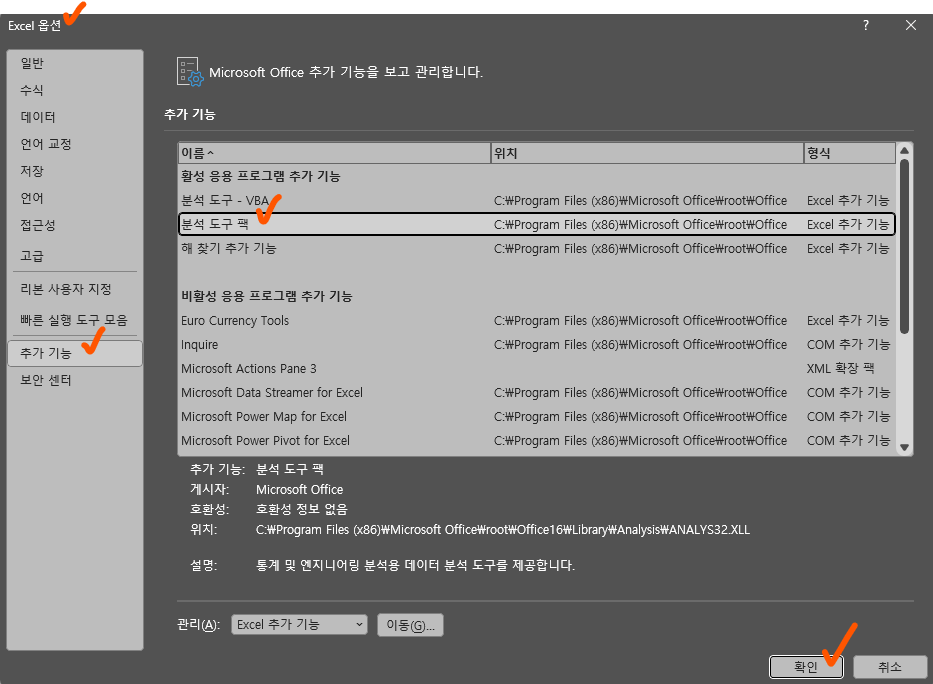
- 데이터 분석 도구 추가
- [파일] → [옵션] → [추가 기능] → [분석 도구] 사용
- [데이터] → [데이터 분석] → F-검정: 두 표본의 분산 비교 선택
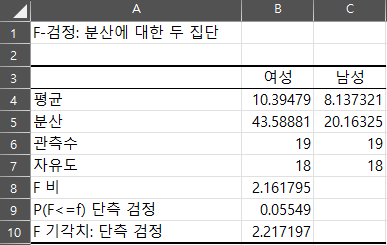
- 각 범위 지정 후 확인 →
- F 통계량, p-값, 임계값이 자동으로 계산


5-2. R / Python 예시
- R
- var.test(group1, group2)
- Python (scipy)
- from scipy.stats import f
F = s1 ** 2 / s2 ** 2
p = 2 * min(f.cdf(F, n1-1, n2-1), 1 - f.cdf(F, n1-1, n2-1))
- from scipy.stats import f
통계 도구를 쓰면 계산 자체보다 결과 해석과 비즈니스 인사이트에 집중할 수 있다.
6. 실무에서의 해석 포인트 정리
마지막으로, F-검정 결과를 업무 관점에서 어떻게 읽으면 좋은지 요약해 보자.
- p-value ≥ 0.05
- “두 집단의 분산은 통계적으로 유의하게 다르다고 보기 어렵다”
- → 등분산 가정 사용, 평균 비교나 ANOVA를 그대로 진행
- p-value < 0.05
- “두 집단의 분산이 다를 가능성이 크다”
- →
- 평균 비교는 Welch t-검정/이분산 t-검정으로 전환
- 공정 관리 측면에서는 변동이 큰 쪽의 원인 분석·개선 활동 수행
즉, F-검정은 “누가 평균이 더 크냐/작으냐”를 바로 말해주는 검정이 아니라,
그 전에 **“두 집단의 안정성(변동성)이 같은 수준인가?”**를 먼저 체크해 주는 기초 안전 점검용 도구라고 이해하면, 실무 통계 분석의 흐름이 훨씬 자연스럽게 잡힌다.
이 관점만 잡아두면, 품질관리·실험 설계·A/B 테스트 등 다양한 상황에서 F-검정을 적절히 배치할 수 있다.
- Total
- Today
- Yesterday
- 건강식
- 나스닥
- 홈쿠킹
- 미국주식투자
- 방학
- 엑셀
- 가정식
- 미국주식전망
- 미국장마감
- 미국증시
- 미국주식
- 미국주식마감
- 팔런티어
- 브로드컴
- 아이와함께
- ai투자
- 집밥
- 바이오주
- 엔비디아
- AI반도체
- 엑셀함수
- 방학간식
- AMD
- 장마감
- 오라클
- 알파벳
- 미국증시마감
- ai테크주
- 팔란티어
- 테슬라
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |

